Drawing circular and non-circular gears for FDM 3d-printing

Gear profile

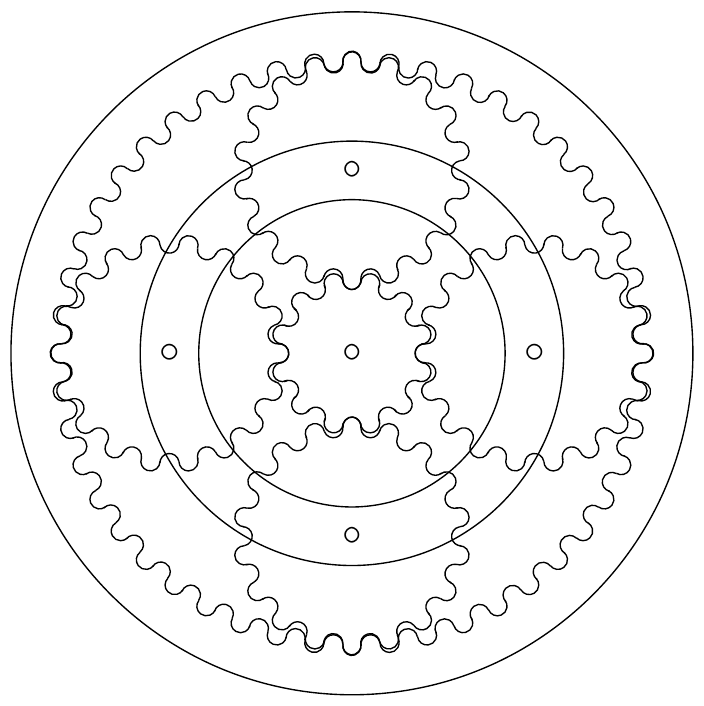
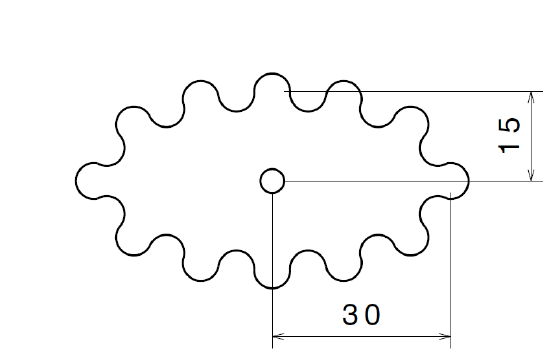
Under normal circumstances, involute gears are the way to go as they offer many advantages when compared to other gear profiles. However, if non-circular gears are required drawing an involute gear profile can become complicated as not all teeth are the same size.

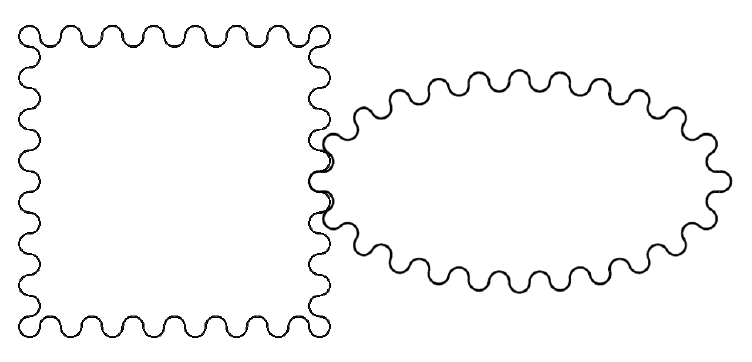
As FDM 3d printed parts are (in general) not as strong as metal parts and therefore torque and transmission efficiency is not as important, we can try to use a different gear profile. If we use circular teeth we ensure that all teeth have the same size regardless of the gear outline.

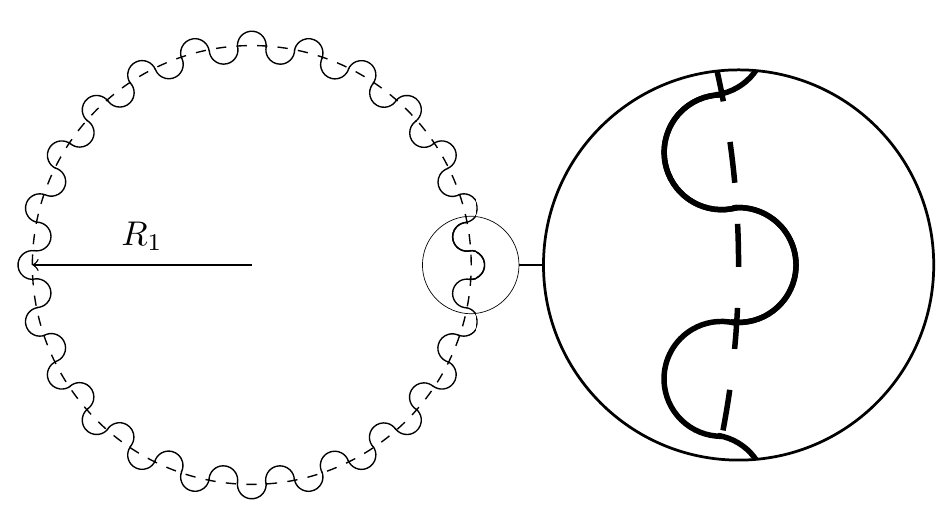
This gear profile is therefore very easy to construct, as you can see in fig. 2 below.

Calculating the correct tooth size

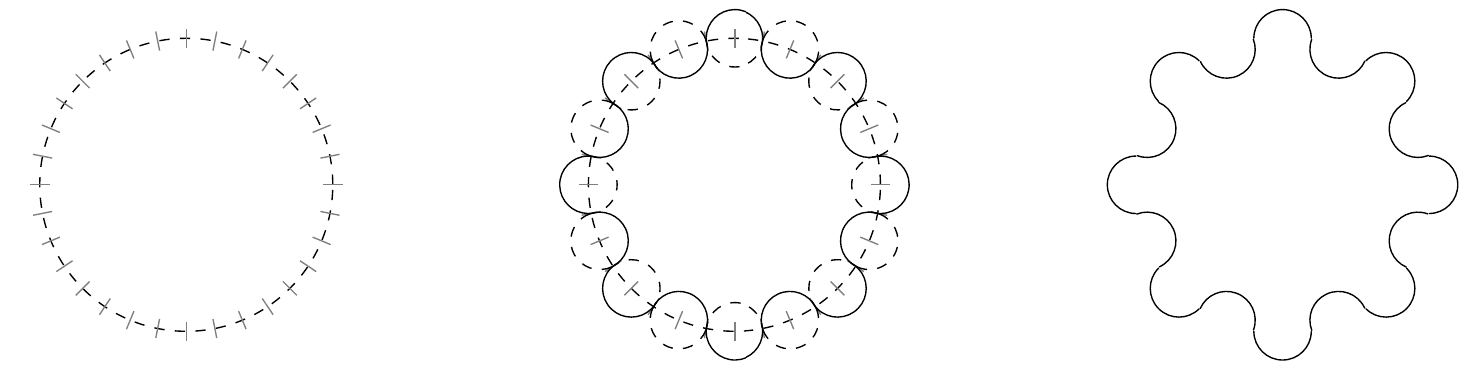
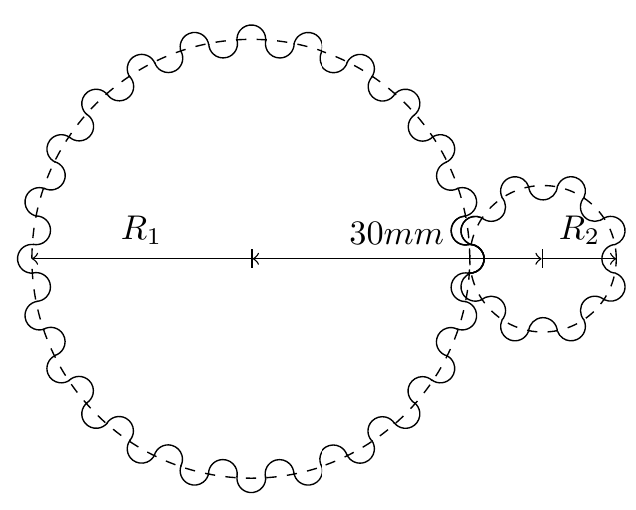
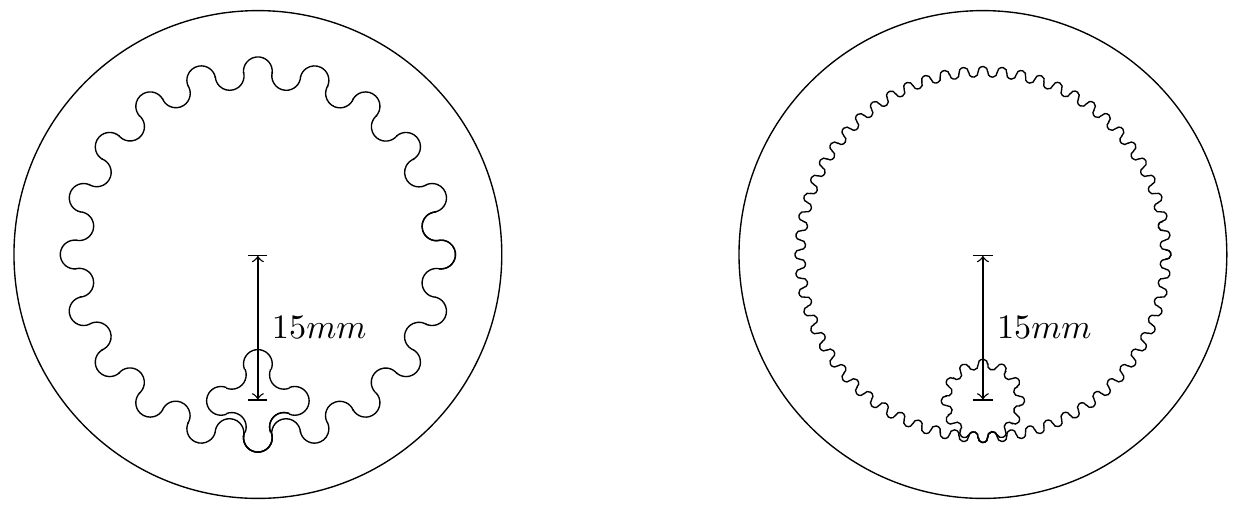
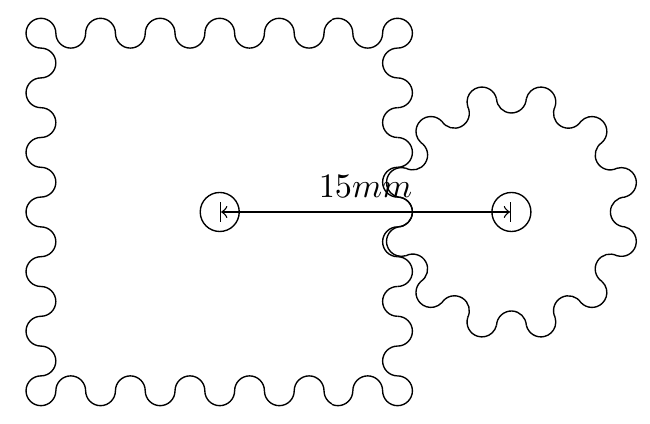
To calculate the required tooth size \(r\) we have to solve a simple system of equations using a computer algebra program like maple for example.

As the required system of equations is dependant on the gear shape, please take a look at the linked PDF paper for more details on how to assemble it.

Examples included in the PDF

The linked PDF paper contains several detailed examples of how to calculate both circular and non circular gears using the proposed gear profile. Listed below are the results of all included examples:

Circular gears with given gear ratio and centerdistance

Internal ring gear

Planetary gearbox (epicyclic gear train)

Rectangular/square gear with given side length

Rectangular and circular gears with given gear ratio and center-distance

Elliptical gear with given size and number of teeth

Elliptical gear and square gear that fit together

Downloads

License

The content published on this page (with exceptions) is published under the CC Attribution-NonCommercial 3.0 Unported License. You are free to share on commercial blogs/websites as long as you link to this page and do not sell material found on blog.hirnschall.net/* or products with said material.