Programming an advanced C++ calculator

Motivation
Goals
How a calculator program works
Basic C++ implementation
Finding Numbers and Operators
Finding Parentheses
Computing the Result
Adding advanced features
Binary Operators like \(a^b\)
Unary Operators like \(\sin(a)\)
Constants like \(\pi\)
Variables like \(\text{ans}\)
Further Ideas
Downloads

Subscribe for New Projects

Motivation

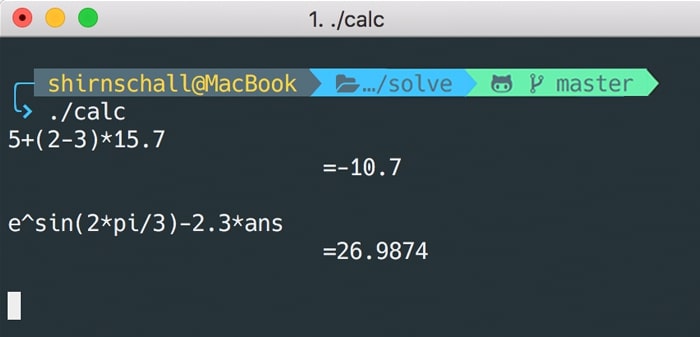
Ever since I started programming, I wanted to write my own calculator program. However, all tutorials and how-tos I could find online were about simple calculators that scan two numbers and either add or multiply them. This is not what I want, and it's probably not what you want either!

Let's take a look at how we can build a c++ calculator that can process an input string (e.g. \(5+2*(3-1)\)) and compute the result of a somewhat complicated calculation, including parentheses. As always, you can download the complete source code for this c++ calculator below.

Goals

As I have already mentioned above, the goal is to take a string or char array as an input and return a float (preferably a double).

Furthermore, the code should run on a microcontroller like an ATMega328 (Arduino) or an ESP8266 with little to no modifications.

How a calculator program works

Although there are many different ways to make a calculator in c++, I think our approach is especially elegant. We'll do the following:

parse the input string to find numbers and binary operations (\(*,/,-,+\))
recursively call our solve function if we find brackets
return result as a floating-point number

Starting with a string \(eq\) our first goal is to find and store numbers and operators in a way that makes it easy to compute the correct result. To do so, we'll use three arrays

\(numbers\): stores each number we find in \(eq\)
\(multIndex\): stores the numbers-index of each number that is to the left of a \(*\) operator
\(plusIndex\): stores the numbers-index of each number that is to the left of a \(+\) operator

Let's take a look at the example input "\(8*3+(2-1)*5+7\)" and the three resulting vectors (=arrays) to better understand how this is going to work:

Note: As we'll later see, we have to parse \(eq\) from right to left.

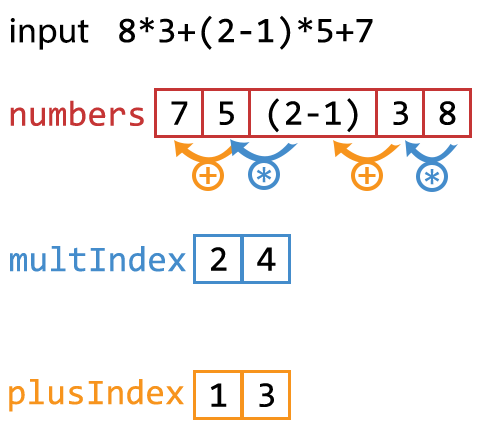
how a c++ calculator console application works with multiplication

As multiplication is done before addition, we'll look at the \(multIndex\) vector first. All we have to do now is to find numbers with their index \(i\) stored in \(multIndex\) and multiply them with the number with index \(i-1\).

We'll then store the result of \(numbers[i]*numbers[i-1]\) in \(numbers[i-1]\) for later use. After this step, our example looks like this:

how a c++ calculator console application works with addition

We can now add all numbers with index in \(plusIndex\) and \(numbers[0]\) together to get the correct result.

If we encounter either a division or a subtraction we can replace them in the following way:

replace \(a/b\) with \(a*\frac{1}{b}\)
replace \(a-b\) with \(a+(-1)*b\)

By parsing \(eq\) from right to left we make sure we know \(b\) as soon as we reach the operator, enabling us to replace \(b\) with either \(-b\) or \(\frac{1}{b}\) as shown above.

Furthermore, we'll include some checks to handle "bad" or incorrect inputs. If we do find a mistake we return \(\text{nan}\) (="Not a Number").

C++ Implementation

Finding Numbers and Operators

I have prepared a minimalist vector class for this project and later use on Arduino. You can find it in the downloads section below or use std::vector instead:

If you don't want to miss my upcoming Arduino calculator build make sure to leave your email below!

Vector<float> numbers;
Vector<char> plusIndex;
Vector<char> multIndex;

To accommodate for subtraction and division, we parse from right to left:

for (char i = end-1; i >= start; --i) {

As C uses ASCII characters it is easy to check if a char is either a digit or the decimal point. If it is, we'll store it in a temporary string tmp:

    if((eq[i]>47 && eq[i]<58) || eq[i]==46){
        if(tmpc>=MAX_NUMBER_LENGTH)
            return std::nanf("");
        tmp[tmpc++]=eq[i];
    }

If we reach a character that is not part of a number we check if it is a known operator, starting with \(+\). If it is, we can convert the tmp string into a number:

    else if(eq[i] == '+'){
        if(tmpc>0){
            reversed=reverseString(tmp,tmpc);
            if(!reversed)
                return std::nanf("");
            plusIndex.push(numbers.push(strtof(reversed,nullptr)));
            free(reversed);
            tmpc=0;
        }
        //handling wrong or weird inputs
        else if(i==end-1){
            return std::nanf("");
        }
        //these two extra cases are necessary because a calculation like a++--+b is valid and equal to a+b
        else if(plusIndex.size() == 0 || (plusIndex.size() > 0 && numbers.size() != *plusIndex.at(plusIndex.size() - 1))){
            plusIndex.push(numbers.size());
        }
    }

Because we are parsing from right to left, tmp is reversed. We can correct this with the following function:

char* reverseString(const char* string,char length){
    auto tmp = (char*)malloc((length+1)*sizeof(char));
    if(!tmp)
        return nullptr;
    tmp[length]='\0';
    for (int i = 0; i < length; ++i) {
        tmp[i]=string[length-1-i];
    }
    return tmp; //make sure to free the returned pointer
}

As we have discussed above we'll replace \(a-b\) with \(a+(-1)*b\). In other words, we multiply the last number we found with \(-1\) and use the same code as with \(+\) above.

    else if(eq[i] == '-'){
        if(tmpc>0){
            reversed=reverseString(tmp,tmpc);
            if(!reversed)
                return std::nanf("");
            plusIndex.push(numbers.push(-strtof(reversed,nullptr)));
            free(reversed);
            tmpc=0;
        }
        //handling wrong or weird inputs
        else if(i==end-1){
            return std::nanf("");
        }
        //these two extra cases are necessary because a calculation like a++--+b is valid and equal to a+b
        else if(plusIndex.size() == 0 || (plusIndex.size() > 0 && numbers.size()!= *plusIndex.at(plusIndex.size() - 1))){
            *numbers.at(numbers.size() - 1)*=-1;
            plusIndex.push(numbers.size());
        }else{
            *numbers.at(numbers.size() - 1)*=-1;
        }
    }

Multiplication and division work in a similar way:

    else if(eq[i]=='*'){
        if(tmpc>0){
            reversed=reverseString(tmp,tmpc);
            if(!reversed)
                return std::nanf("");
            multIndex.push(numbers.push(strtof(reversed,nullptr)));
            free(reversed);
            tmpc=0;
        }else if(i==end-1 || i==start){
            return std::nanf("");
        }
        //this case is for a*-b. because - is pushed into the plusIndex array we need to remove it.
        else if(plusIndex.size()>0 && *plusIndex.at(plusIndex.size()-1) == numbers.size()){
            plusIndex.pop();
            multIndex.push(numbers.size());
        }
        else{
            multIndex.push(numbers.size());
        }
    }else if(eq[i]=='/'){
        if(tmpc>0){
            reversed=reverseString(tmp,tmpc);
            if(!reversed)
                return std::nanf("");
            multIndex.push(numbers.push((float)1/strtof(reversed,nullptr)));
            free(reversed);
            tmpc=0;
        }else if(i==end-1 || i==start){
            return std::nanf("");
        }
        //this case is for a/-b. because - is pushed into the plusIndex array we need to remove it.
        else if(plusIndex.size()>0 && *plusIndex.at(plusIndex.size()-1) == numbers.size()){
            plusIndex.pop();
            (*numbers.at(numbers.size() - 1)) = 1 / (*numbers.at(numbers.size() - 1));
            multIndex.push(numbers.size());
        }else{
            (*numbers.at(numbers.size() - 1)) = 1 / (*numbers.at(numbers.size() - 1));
            multIndex.push(numbers.size());
        }
    }

If we divide by zero C returns \(inf\).

Finding Parentheses

If we find a closing bracket ')' we'll look for a matching open bracket '('. Once we find a matching pair we can recursively call \(solve(eq,\text{index of '('}+1,\text{index of ')'})\):

    else if(eq[i]==')'){
        //try to find a matching '(':
        char numClosingBrackets=0;
        char foundMatching=0;
        for(char j=i-1;j>=start;--j){
            if(eq[j]==')')
                ++numClosingBrackets;
            else if(eq[j]=='(' && numClosingBrackets>0)
                --numClosingBrackets;
            else if(eq[j]=='(' && numClosingBrackets==0){
                //matching '(' found
                if(!foundMatching) {
                    numbers.push(solve(eq, j + 1, i,vars));
                    i = j;//skip the part between () in parsing
                    foundMatching = 1;
                }
            }
        }
            if(!foundMatching)
                return std::nanf("");
    }
}

After we are done parsing the whole string we have to convert tmp to a number one last time:

    if(tmpc>0){
        reversed=reverseString(tmp,tmpc);
        if(!reversed)
            return std::nanf("");
        numbers.push(strtof(reversed,nullptr));
        free(reversed);
        tmpc=0;
    }

Computing the result

Now all that's left to do is computing the result. We'll start with multiplication and division. As we changed each division into a multiplication, it does not matter if we go from right to left or from left to right. We'll go from right to left and always replace the left number with the result.

As we are using pointers we have to dereference them using the *-operator:

    if(numbers.size()==0)
        return std::nanf("");
    if(multIndex.size() > 0) {
        for (char i = multIndex.size()-1;i>=0  ; --i){
            //check if '*' is associated with two numbers:
            if(*multIndex.at(i)>= numbers.size())
                return std::nanf("");
            (*numbers.at(*multIndex.at(i)-1)) *= (*numbers.at(*multIndex.at(i)));
        }
    }

As we have always replaced the left number with the result, we can now add all numbers that are to the right of a \(+\)-operator. We also have to include the leftmost number.

    float result=*numbers.at(0);
    for (char i=0;i< plusIndex.size(); ++i){
        result+=*numbers.at(*plusIndex.at(i));
    }
    return result;
}

And we are done!

Well, now that we have a simple calculator program working, let's take a look at how we can implement some more advanced features.

Adding advanced features

Although not absolutely necessary, we always want to avoid computationally complex code. So, if possible, we would rather not:

resize an array
have unnecessarily large arrays (store data more than once)
remove elements from the middle of an array (we would much rather ignore existing elements if we can)
have nested loops (this can result from badly structured arrays, if possible, we want linear complexity)
write complicated code with many ifs, else ifs

Let's now take a look at two different implementations of a power function to get a better understanding of what we might want to avoid when expanding our basic c++ calculator.

Binary Operators like power (\(a^b\))

Let the input string \(eq\) contain \(\text{a^b}\).

1. possible implementation:

As we are parsing from right to left, we know \(b\) once we reach the '^' char. We now set a flag (e.g. \(\text{powFound}=\text{true}\)) and continue parsing. Every time we reach an operator, we check if the flag is set. If it is, we replace \(b\) with the value of \(a^b\) as we now know both \(a\) and \(b\).

Pros:

No array manipulations
No nested for loops

Cons:

If case for every operator we are using \(\implies\) “the same” code in multiple different places
Not really the same logic as multiplication and addition

2. possible implementation:

We add a new array \(\text{powIndex}\). If we encounter a '^' char, we push the numbers-array’s current length into both the \(\text{powIndex}\) and the \(\text{multIndex}\) array.

Now, before we do the multiplication step we can compute \(a^b\), replace \(a\) with the result, and \(b\) with \(1\). We then continue with multiplication as usual.

Pros:

We do not need to change existing code
No array manipulations
No nested for loops
No if else
Logically the same as addition and multiplication
All code in one location
We can use the same logic for other binary operators

Cons:

We need a new array
We are doing one unnecessary multiplication per pow

As the number of '^' chars in a single calculation is very low, I would definitely prefer the second approach to implement operators in this basic c++ calculator.

The code is fairly simple:

    else if(eq[i]=='^'){
        if(tmpc>0){
            reversed=reverseString(tmp,tmpc);
            if(!reversed)
                return std::nanf("");
            multIndex.push(numbers.push(strtof(reversed,nullptr)));
            powIndex.push(numbers.size());
            free(reversed);
            tmpc=0;
        }else if(i==end-1 || i==start){
            return std::nanf("");
        }else{
            multIndex.push(numbers.size());
            powIndex.push(numbers.size());
        }
    }

    if(powIndex.size() > 0) {
        for (char i = powIndex.size()-1;i>=0; --i){
            //check if '*' is associated with two numbers:
            if(*powIndex.at(i)>= numbers.size())
                return std::nanf("");
            (*numbers.at(*powIndex.at(i)-1)) = pow((*numbers.at(*powIndex.at(i))),(*numbers.at(*powIndex.at(i)-1)));
            (*numbers.at(*powIndex.at(i))) = 1;
        }
    }

Unary Operations like \(\sin(a)\)

Adding unary operators or functions is very easy. As we have mentioned numerous times above, we always know the number to the right of an operator by the time we reach the operator. So, all we need to do is check if we find a new operator and replace the last number we found. You can see an example with sine and arcsine below:

    else{
        //unary operators:
        //trig functions work with rad not deg!
        if(i>2 && eq[i]=='n' && eq[i-1]=='i' && eq[i-2]=='s' && eq[i-3]=='a'){
            if(numbers.size())
                *numbers.at(numbers.size()-1) = asin(*numbers.at(numbers.size()-1));
            i-=3;
            if(plusIndex.size()>0 && *plusIndex.at(plusIndex.size()-1) == numbers.size()) {
                plusIndex.pop();
            }
        }else if(i>1 && eq[i]=='n' && eq[i-1]=='i' && eq[i-2]=='s'){
            if(numbers.size())
                *numbers.at(numbers.size()-1) = sin(*numbers.at(numbers.size()-1));
            i-=2;
            if(plusIndex.size()>0 && *plusIndex.at(plusIndex.size()-1) == numbers.size()) {
                plusIndex.pop();
            }
        }else
            return std::nanf("");
    }

Constants like \(\pi\)

Implementing constants is almost the same as implementing unary functions. Instead of changing the last number in \(\text{numbers}\) we push the value of the constant we found.

Example implementation of \(\pi\) as a constant:

    //constants
    else if(i>0 && eq[i]=='i' && eq[i-1]=='p'){
        if(numbers.size())
            numbers.push(M_PI);
        i-=1;
    }

Depending on the number of constants we want to add, we might want to store them in a matrix and use a loop to check which one we found.

Variables like \(\text{ans}\)

It can be quite useful to use the last result or to save a result for later use. We'll first change the prototype of our solve function to receive a pointer to where the variables are stored:

float solve(const char* eq,char start,char end,const float* vars = nullptr);

We can then use almost the same source code as above:

    else if(i>1 && eq[i]=='s' && eq[i-1]=='n' && eq[i-2]=='a'){
        if(vars)
            numbers.push(vars[0]);
        else
            numbers.push(std::nanf(""));
        i-=2;
    }

By implementing variables in this way, we have to be very careful that the specified array is the correct size! We also have to map each variable we want to use to an index (e.g. \(\text{ans}\) is stored at index \(0\)).

If you have any questions or find a mistake feel free to comment on GitHub or use the contact form in the top right corner of the screen to message me directly!

Further Ideas

Now that you have your basic c++ calculator working, try implementing:

fractions. Instead of returning a double or float, you could work with your own fraction class to get exact results. (Tip: take a look at continued fractions for typecasting a double to a fraction)
better support for wrong inputs. Try either return an error or fix the input.
this function in a c++ calculator class

As always feel free to share your changes on GitHub!

Get Notified of New Articles

Subscribe to get notified about new projects. Our Privacy Policy applies.